本篇文章来源于前期发布的视频根据AI总结生成的精华点阅读!
## 摘要
本视频详细讲解了尺寸公差体系中的尺寸链计算方法及其局限性。吴德辉老师首先介绍了尺寸链计算的三大步骤,包括确定封闭环、组成环、增环和减环,以及如何处理数据计算封闭环的尺寸和公差。随后,视频深入探讨了尺寸公差的四大主要局限性,包括被测要素和基准要素不明确、公差累加、公差带变小导致成本增加以及无法实现精准设计。最后,视频明确了尺寸公差的适用范围,建议仅用于定义尺寸要素的尺寸,其他情况应优先考虑几何公差。
### 视频亮点
- 尺寸链计算涉及三大步骤:首先将所有尺寸公差转换为对称公差,接着确定封闭环、组成环、增环和减环并绘制矢量图,最后处理数据计算封闭环的尺寸和公差 [10:35]。
- 尺寸公差的一个主要局限性在于其被测要素和基准要素不明确,这可能导致供应商与客户之间在测量结果的合格性上产生争议 [13:30]。
- 尺寸公差体系下容易产生公差累加,特别是在孔组等特征的管控中,导致整体公差范围扩大,可能影响零件的装配,而几何公差(如位置度)能有效避免此问题 [15:45]。
- 尺寸公差的公差带通常是正方形,相比几何公差的圆形公差带,面积更小,导致实际可用但按尺寸公差却不合格的情况,从而造成不必要的成本浪费 [20:30]。
- 尺寸公差无法实现精准设计,因为它不能将孔径与位置度等关联起来,而几何公差结合实体要求(如M圈)可以解决这一问题,允许在孔做大时适当偏离位置,只要不影响装配即为合格 [21:58]。
### 思考
1. 尺寸链计算中的“封闭环”和“组成环”分别指什么?
- 封闭环是指未被直接管控、被动形成的尺寸,其变化范围受其他尺寸决定。组成环是指直接管控的尺寸,它们共同决定了封闭环。
2. 为什么说尺寸公差的公差带比几何公差小,会导致成本提高?
- 尺寸公差的公差带通常呈方形,而几何公差(如位置度)的公差带可以是圆形。在某些情况下,实际零件中心轴线落在圆形公差带内但在方形公差带外的区域,虽然功能上可能合格,但按尺寸公差的判定却是不合格的,这导致了额外的报废,从而增加了生产成本。
### 术语解释
-**尺寸链**: 指在零件或产品设计中,一系列相互关联的尺寸及其公差,它们共同影响某个关键尺寸或特征的累积变化范围。
-**封闭环**: 尺寸链中未被直接标注公差,其数值和公差由其他直接标注公差的尺寸(即组成环)决定的尺寸。
-**组成环**: 尺寸链中直接被标注公差的尺寸,它们是决定封闭环的直接因素。
-**增环/减环**: 在尺寸链计算中,根据组成环的尺寸方向与封闭环方向的相对关系来定义的,方向相同为增环,方向相反为减环。
-**几何公差**: 一种用于控制零件形状、方向、位置和跳动误差的公差标注方法,相比尺寸公差能更精确地表达设计意图,并明确基准要素和被测要素。
## 视频章节总结 | 尺寸链计算与公差累加原理:为什么尺寸公差会失效?几何公差如何破局?
本视频深入探讨了尺寸公差体系中的尺寸链计算方法及其固有的局限性,并提出了几何公差作为解决方案。首先,视频详细讲解了尺寸链的计算步骤,包括确定封闭环、设置起始点与终止点、确定正方向、绘制矢量图以及判断增环与减环,最终得出封闭环的尺寸与公差计算公式。通过尺寸链的累加效应,强调了减少组成环数量和直接标注关键尺寸的重要性。其次,视频剖析了尺寸公差的四大局限性:被测要素和基准要素不明确易引发争议;公差累加导致尺寸偏差放大,影响装配;公差带呈正方形,空间利用率低,造成不必要的报废和成本浪费;以及无法实现精准设计,特别是在孔径与位置关联性上存在缺陷。最后,视频指出尺寸公差仅适用于定义尺寸要素的尺寸,而在需要明确基准、避免累加、优化公差带或实现精准设计时,应优先采用几何公差,从而提升产品质量、降低成本并优化生产过程。
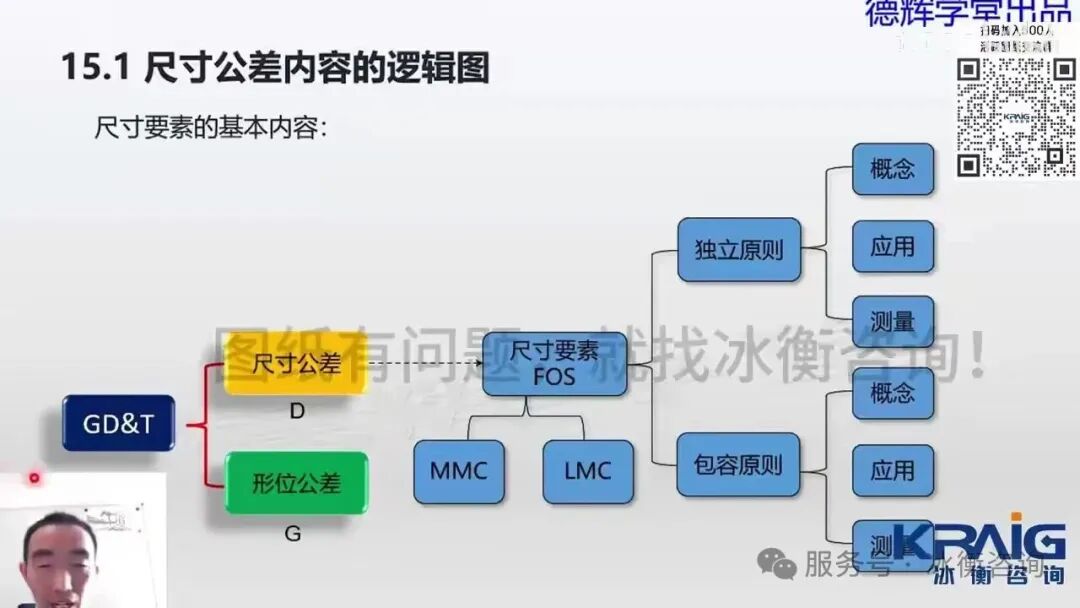
尺寸链计算基础与核心概念[00:00]
本章首先介绍了尺寸链计算的背景和目的:确定封闭环的变化范围。详细阐述了计算的五大步骤:确定封闭环(未被直接管控的尺寸)、设置起始点和终止点、设置正方向、绘制矢量图以区分组成环(增环和减环),并最终展示了如何将组成环的尺寸和公差列入表格,转换为对称公差,进而计算封闭环的尺寸部分(增环之和减去减环之和)和公差部分(所有组成环公差之和)。强调了公差累加的现象。
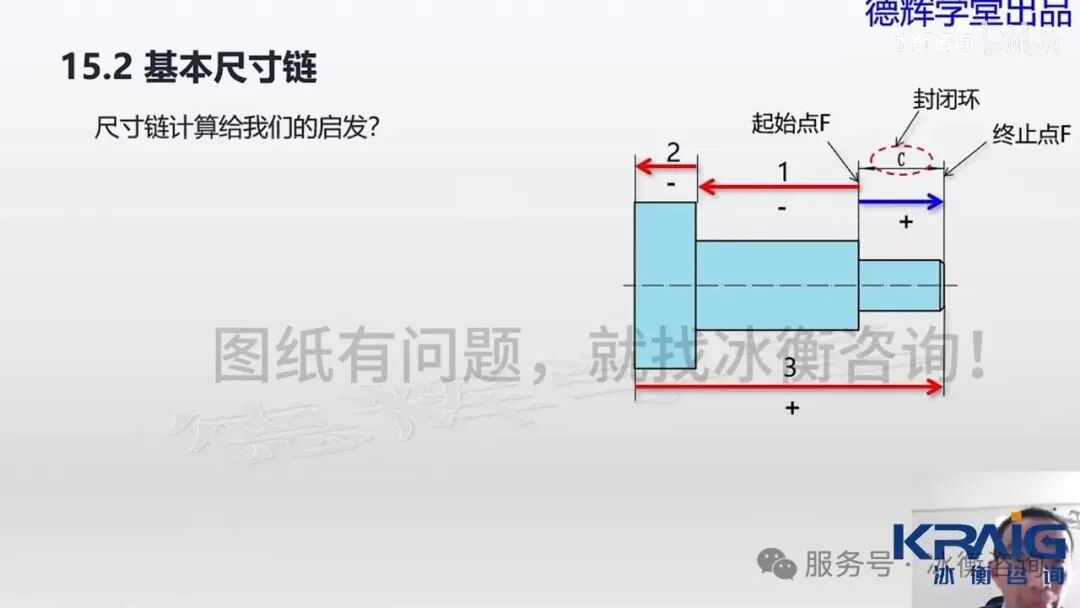
[05:08]尺寸链计算的设计启示
通过尺寸链计算,设计工程师可以得到重要启发。第一,封闭环的公差等于组成环的公差之和,意味着组成环越多,公差累加越大。因此,应尽可能减少组成环数量。第二,关键尺寸应尽可能直接标注,避免公差累加。第三,应将封闭环设置在相对不重要的位置,以减少对功能的影响。本章总结了尺寸链计算的三大步骤:尺寸公差对称化、确定封闭环和组成环并画矢量图、以及数据处理计算封闭环的尺寸和公差。
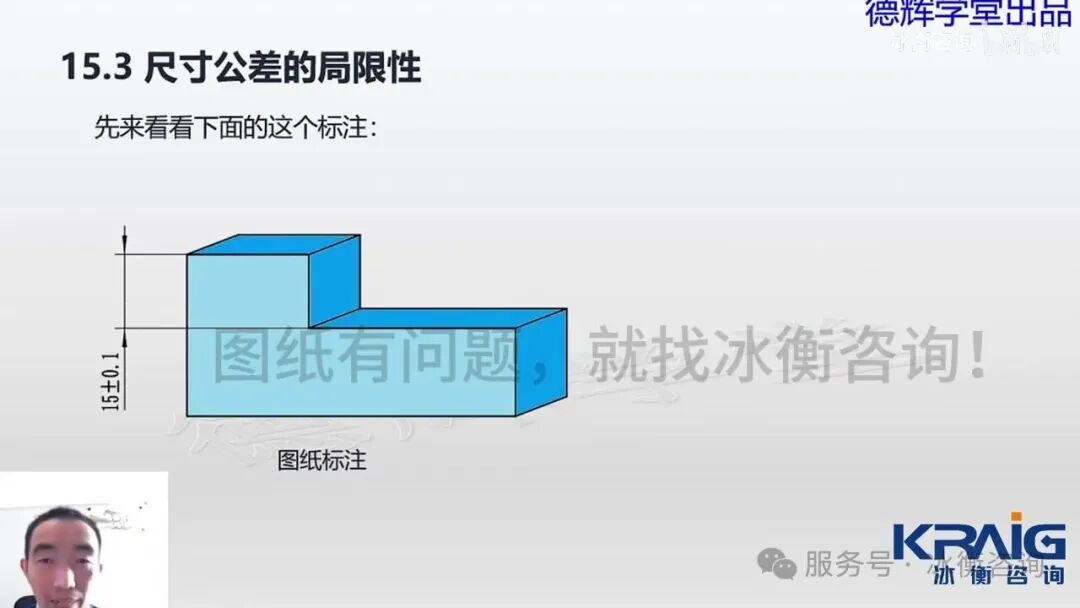
[07:43] 局限性一:基准与被测要素不明确
本章深入探讨了尺寸公差的第一个局限性:被测要素和基准要素不明确。通过一个台阶零件的案例,演示了在无明确基准时,供应商和客户可能因不同的测量方式(以A面或B面为基准)导致对零件合格性的判断出现争议。同样,对于两个孔的中心距标注,尺寸公差也无法明确测量时应以哪个孔为基准。几何公差(如轮廓度或位置度)则能有效解决这一问题,通过明确基准要素和被测要素,使制造和测量要求一目了然。
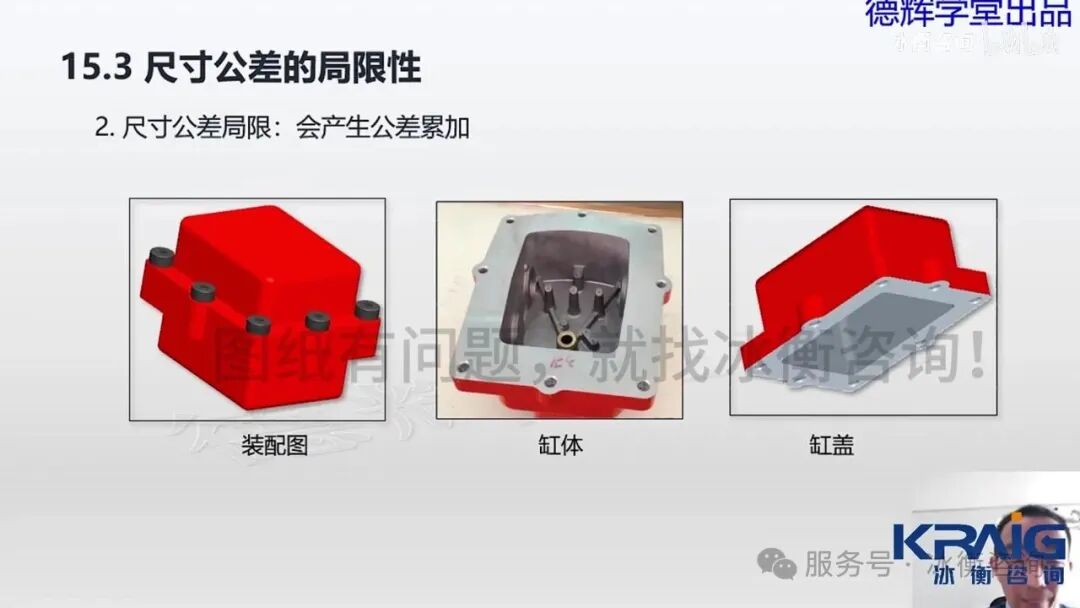
[11:18] 局限性二:公差累加的危害
尺寸公差的第二个局限性是公差累加。以变速箱缸盖上的螺钉孔组为例,传统的尺寸公差标注方法(如相邻孔中心距±0.1)看似合理,但通过尺寸链计算,发现非相邻孔(如A、C孔)的中心距变化范围会因累加效应而显著增大,甚至超出设计预期,导致螺钉无法正常装配。这种公差累加对装配带来巨大挑战。几何公差(如位置度)则能有效解决公差累加问题,通过整体控制孔组的相对位置,确保任意两个孔之间的中心距变化范围都在可控范围内,从而保证装配的顺畅性。

[15:51] 局限性三:公差带效率低下与成本浪费
本章揭示了尺寸公差的第三个局限性:公差带呈正方形,空间利用率低,导致不必要的成本浪费。以一个钣金件的孔为例,尺寸公差将孔的公差带定义为正方形区域,使得实际孔中心轴线落在角落的绿色弓形区域时被判为不合格,尽管这些孔在功能上是可用的。这种“误判”导致了浪费。采用几何公差(如位置度)时,公差带是一个圆形区域,面积比尺寸公差的正方形公差带更大,且能更合理地反映实际功能需求,从而提高合格率并降低制造成本,实现了更经济的设计。
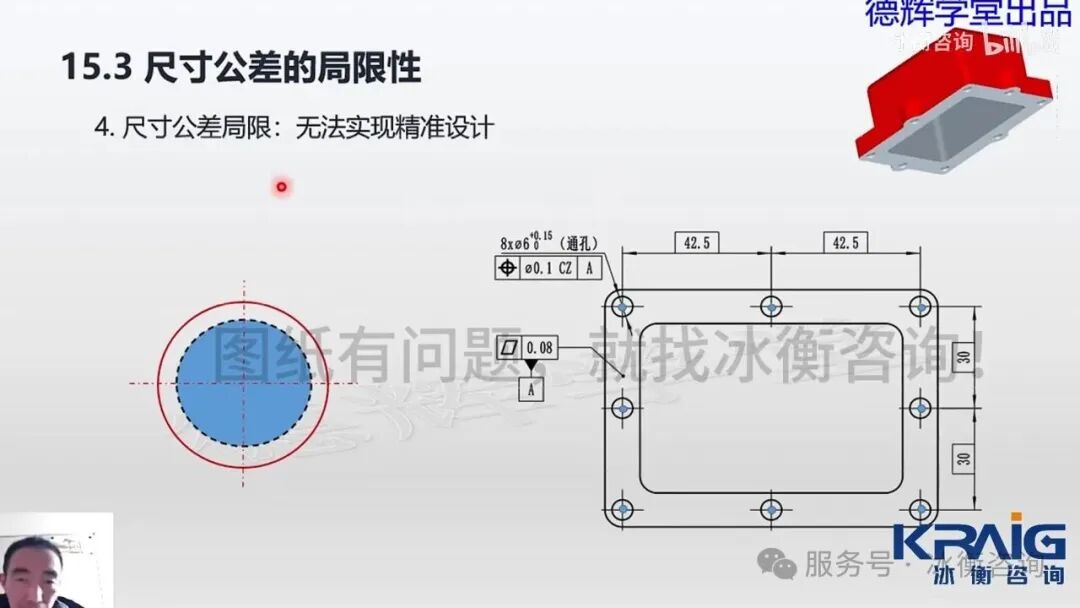
[18:29]局限性四:无法实现精准设计
尺寸公差的第四个局限性是无法实现精准设计,特别是在孔径与位置的关联性上。以缸盖螺钉过孔为例,即使过孔直径做大且位置偏移超出了位置度公差带,但只要螺钉与过孔之间的最小间隙仍大于零,螺钉依然可以顺利穿过。然而,按照尺寸公差标准,这样的零件却被判为不合格。几何公差结合实体要求(M圈)则能解决此问题,允许在零件实际尺寸更利于装配时,放宽位置公差,从而实现更精准的设计,即“只要零件能够装配,就认为是合格的”,而尺寸公差无法实现这种关联性。

[21:03] ✅ 尺寸公差的适用范围与总结回顾
鉴于尺寸公差的诸多局限性,本章明确指出其理想适用范围:仅用于定义尺寸要素的尺寸,如孔、轴、板、槽、球的尺寸。在其他需要明确基准、避免公差累加、优化公差带或实现精准设计的功能性要求上,应优先采用几何公差。最后,视频回顾了本讲的三个核心内容:尺寸链的计算三步法、尺寸公差的四大局限性(基准不明确、公差累加、公差带小、无法精准设计),以及尺寸公差的正确适用范围。
基于新的模式的尝试大家有什么好的建议吗?欢迎下方留言或者添加客服微信告知我们,非常感谢!
 我们12月份还有年内最后一期的GD&T公开课,有兴趣的学员联系客户获取优惠信息!
我们12月份还有年内最后一期的GD&T公开课,有兴趣的学员联系客户获取优惠信息!
总有一群老法师,执着于最前沿的研发和质量领域,为中国制造业增强竞争力
专注研发流程优化和质量改善 - 冰衡中国

他们是:
研发流程专家
GD&T专家
CQI专家
创新设计思维专家
质量专家
...
他们是业界资深而低调的实战专家




